In the last post I discussed the Rabin Karpe algorithm for substring matching. While this algorithm exhibits a best case complexity of O(n) [where n is the size of the text], using hash functions for string matching has certain limitations. A hash function relies on us knowing the exact length of the pattern. What if you don’t know how long the pattern x is going to be? In cases where the pattern varies, using a suffix tree makes a lot of sense.
Suffix trees are much faster when the text is fixed and known first while the patterns vary.
Time Complexity: O(m) for single time processing the text, then only O(n) for each new pattern.
In the rest of the post, I am going to describe what a suffix tree is, how to construct and query it.
Prefixes & Suffixes
For a string S:
S=AACTAG
Prefixes: AACTAG,AACTA,AACT,AAC,AA,A
Suffixes: AACTAG,ACTAG,CTAG,TAG,AG,G
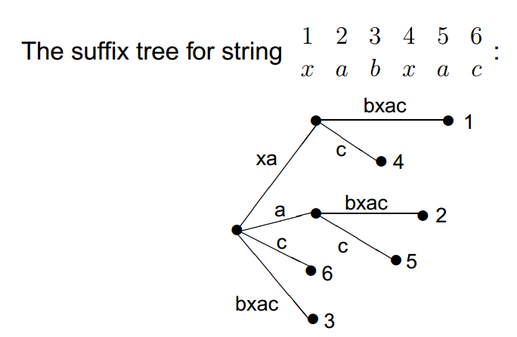
P is a substring of S if P is a prefix of some suffix of S. Suffix Trees exploit this property of strings to solve the substring pattern matching problem.
Suffix Tree
A suffix tree ST for an m-character string S is a rooted directed tree with exactly m
leaves numbered 1 to m. Each internal node, other than the root, has at least two children and each edge is labeled with a nonempty substring of S.
The key feature of the suffix tree is that for any leaf i, the concatenation of the edge-labels on the path from the root to the leaf i exactly spells out the suffix of S that starts at position i.
Suffix trees are much faster when the text is fixed and known first while the patterns vary.
Time Complexity: O(m) for single time processing the text, then only O(n) for each new pattern.
In the rest of the post, I am going to describe what a suffix tree is, how to construct and query it.
Prefixes & Suffixes
For a string S:
- Prefix of S: substring of S beginning at the first position of S
- Suffix of S: substring that ends at its last position.
S=AACTAG
Prefixes: AACTAG,AACTA,AACT,AAC,AA,A
Suffixes: AACTAG,ACTAG,CTAG,TAG,AG,G
P is a substring of S if P is a prefix of some suffix of S. Suffix Trees exploit this property of strings to solve the substring pattern matching problem.
Suffix Tree
A suffix tree ST for an m-character string S is a rooted directed tree with exactly m
leaves numbered 1 to m. Each internal node, other than the root, has at least two children and each edge is labeled with a nonempty substring of S.
The key feature of the suffix tree is that for any leaf i, the concatenation of the edge-labels on the path from the root to the leaf i exactly spells out the suffix of S that starts at position i.
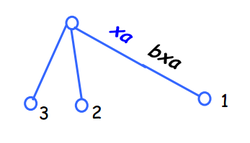
Does a suffix tree always exist? Not necessarily.
If one suffix Sj of S matches a prefix of another suffix Si of S, then the path for Sj would not end at a leaf.
Example:
S = xabxa
S1 = xabxa and S4 = xa. In this case, the suffix S4 is also a prefix of suffix S1.
How to avoid this problem?
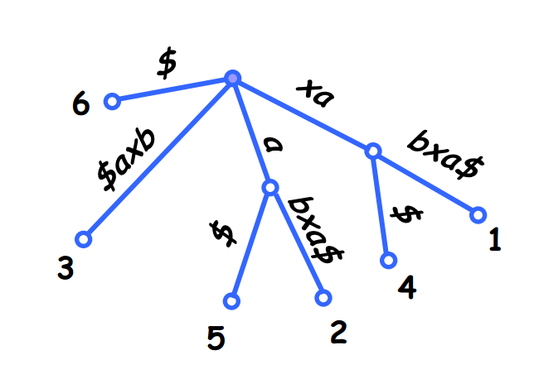
Suffix Tree for S= xabxa$
If one suffix Sj of S matches a prefix of another suffix Si of S, then the path for Sj would not end at a leaf.
Example:
S = xabxa
S1 = xabxa and S4 = xa. In this case, the suffix S4 is also a prefix of suffix S1.
How to avoid this problem?
- Assume that the last character of S appears nowhere else in S.
- Add a new character $ not in the alphabet to the end of S.
Suffix Tree for S= xabxa$
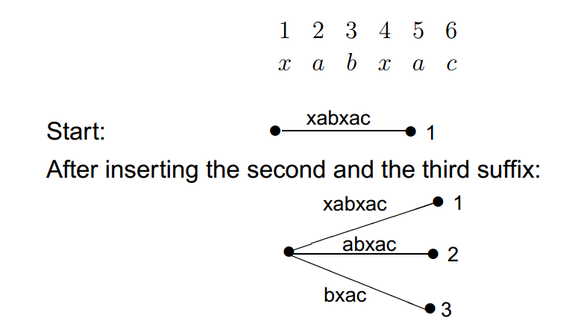
How to Construct a Suffix Tree (Naive Method)
Let us first build a suffix tree the naive way.
Let us first build a suffix tree the naive way.
Time Complexty: Naïve method - O(m2) (m = text size)
CODE:
Here's an excellent implementation of the suffix tree described above:http://en.literateprograms.org/Suffix_tree_(Java) and
http://en.literateprograms.org/Special:DownloadCode/Suffix_tree_(Java)
In the next post, I will discuss Ukkonen’s linear-time construction that takes time O(m) to build a suffix tree.
REFERENCES:
CODE:
Here's an excellent implementation of the suffix tree described above:http://en.literateprograms.org/Suffix_tree_(Java) and
http://en.literateprograms.org/Special:DownloadCode/Suffix_tree_(Java)
In the next post, I will discuss Ukkonen’s linear-time construction that takes time O(m) to build a suffix tree.
REFERENCES:
- http://www.stanford.edu/~mjkay/gusfield.pdf
- http://www.cs.ucf.edu/~shzhang/Combio11/lec3.pdf
- http://www.cs.duke.edu/courses/fall12/compsci260/resources/suffix.trees.in.detail.pdf


 RSS Feed
RSS Feed
