Breadth-first search (BFS) is a graph traversal algorithm that explores nodes in the order of their distance from the roots. Here distance is defined as the minimum path length from a root to the node. Its pseudo-code would look something like:
Here the white nodes are those not marked as visited, the gray nodes are those marked as visited and that are in frontier, and the black nodes are visited nodes no longer in frontier. Rather than having a visited flag, we can keep track of a node's distance in the field v.distance. When a new node is discovered, its distance is set to be one greater than its predecessor v.
Basically, when frontier is a first-in, first-out (FIFO) queue, we get breadth-first search. All the nodes on the queue have a minimum path length within one of each other. In general, there is a set of nodes to be popped off, at some distance k from the source, and another set of elements, later on the queue, at distance k+1.
Basically, when frontier is a first-in, first-out (FIFO) queue, we get breadth-first search. All the nodes on the queue have a minimum path length within one of each other. In general, there is a set of nodes to be popped off, at some distance k from the source, and another set of elements, later on the queue, at distance k+1.
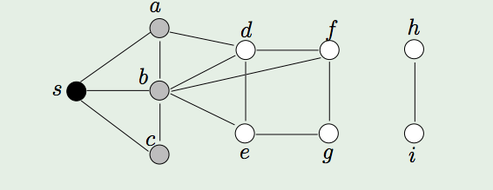
Here's a small example. In the graph above, our root is S.
- At the beginning, color all the vertices white
- Initiate an empty queue Q
- Add the node S to the frontier. Color it gray.
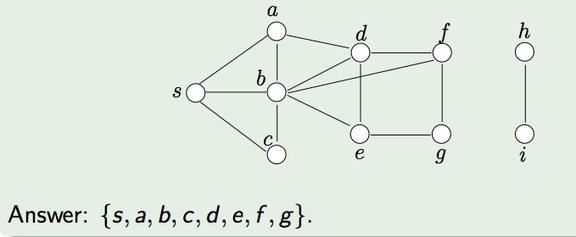
3. Remove S. Mark it as Black.
4. Mark all its white neighbors (a,b,c) as gray and add them to the frontier.
5. The rest of the algorithm simply repeats the above until Q is empty.
Time Analysis
Let us assume that the input graph G is stored with an adjacency list.
- Coloring all vertices white (at the beginning of BFS) takes O(|V |) time, where V is the set of vertices in G.
- Then, every edge in E (the set of edges in G) is processed at most twice.
- Therefore, the total running time is O(|V | + |E|).
Depth-first search (DFS) : What if we were to replace the FIFO queue with a LIFO stack? In that case we get a completely different order of traversal, namely DFS. With a stack, the search will proceed from a given node as far as it can before backtracking and considering other nodes on the stack.
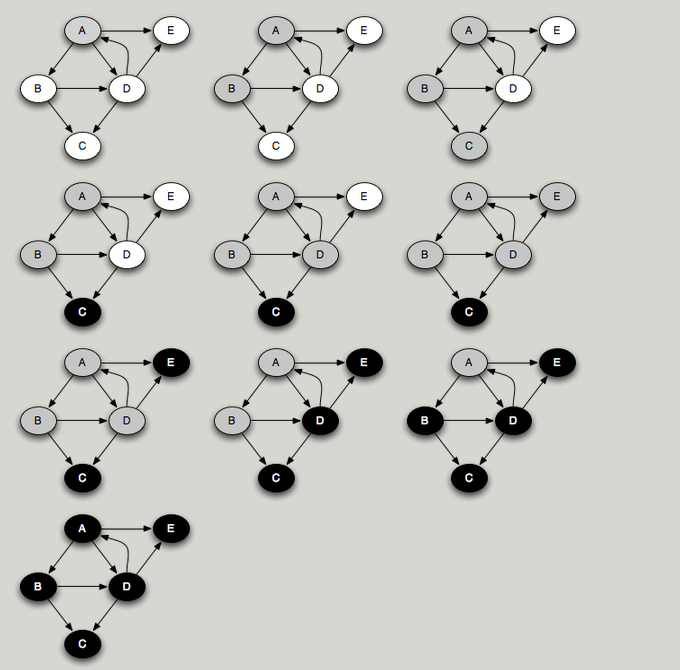
You can think of DFS as a person walking through the graph following arrows and never visiting a node twice except when backtracking, when a dead end is reached. The diagram below shows the DFS traversal of a graph starting from node A.
Time Analysis
Let us assume that the input graph G is stored with an adjacency list.
B C
D
E
Note:
If we want to search the whole graph, then a single recursive traversal may not suffice. If we had started a traversal with node C, we would miss all the rest of the nodes in the graph. To do a depth-first search of an entire graph, we call DFS on an arbitrary unvisited node, and repeat until every node has been visited.
Graph Representation : Adjacency List Vs Adjacency Matrix
A graph can be stored either as a matrix or a list of nodes. The correct choice depends on the problem.
Topological Sort
One of the most useful algorithms on graphs is topological sort, in which the nodes of an acyclic graph are placed in an order consistent with the edges of the graph. This is useful when you need to order a set of elements, for example, suppose you have a set of tasks to perform, but some tasks have to be done before other tasks can start. In what order should you perform the tasks? This problem can be solved by representing the tasks as nodes in a graph, where there is an edge from task 1 to task 2 if task 1 must be done before task 2. Then a topological sort of the graph will give an ordering in which task 1 precedes task 2. Obviously, to topologically sort a graph, it cannot have cycles.
A key observation in Topological Sorting is that a node finishes (is marked black) after all of its descendants have been marked black. Therefore, a node that is marked black later must come earlier when topologically sorted. For example, in the traversal example above, nodes are marked black in the order C, E, D, B, A. Reversing this, we get the ordering A, B, D, E, C. This is a topological sort of the graph. Interestingly enough, a postorder traversal generates nodes in the reverse of a topological sort.
Algorithm:
The algorithm for Topological sort is similar to DFS.
Detecting Cycle
We can use the idea of Topological sorting to detect a cycle in a graph. Since a node finishes after its descendants, a cycle involves a gray node pointing to one of its gray ancestors that hasn't finished yet. If one of a node's successors is gray, there must be a cycle.
To detect cycles in graphs, therefore, we choose an arbitrary white node and run DFS. If that completes and there are still white nodes left over, we choose another white node arbitrarily and repeat. Eventually all nodes are colored black. If at any time we follow an edge to a gray node, there is a cycle in the graph. Therefore, cycles can be detected in O(|V+E|) time.
Java Code:
In the example code below, the sample graph used is quite relatively dense and hence I use an adjacency matrix to represent the graph. To quickly look up a vertex, i enforce the following naming convention/lookup convention:
a b c d e f g h i j k
0 1 2 3 4 5 6 7 8 9 10
so the vertex 'a' is stored at index 0 in the array of vertices. An edge between vertex 'a' and 'b' would hence be an edge between 0 and 1.
Let us assume that the input graph G is stored with an adjacency list.
- There can be at most |V| calls to DFS_visit
- Then, every edge in E (the set of edges in G) is processed at most twice.
- Therefore, the total running time is O(|V | + |E|), same a BFS.
- The sequence of calls to DFS forms a tree. For the graph above the tree is:
B C
D
E
- So the DFS algorithm maintains an amount of state that is proportional to the size of this path from the root. On a balanced binary tree, DFS maintains state proportional to the height of the tree, or O(log |V|).
- In BFS, where the amount of state (the queue size) corresponds to the size of the perimeter of nodes at distance k from the starting node. In both algorithms the amount of state can be O(|V|) in the worst case.
Note:
If we want to search the whole graph, then a single recursive traversal may not suffice. If we had started a traversal with node C, we would miss all the rest of the nodes in the graph. To do a depth-first search of an entire graph, we call DFS on an arbitrary unvisited node, and repeat until every node has been visited.
Graph Representation : Adjacency List Vs Adjacency Matrix
A graph can be stored either as a matrix or a list of nodes. The correct choice depends on the problem.
- An adjacency matrix uses O(n*n) memory, where n is the number of nodes.
- It has fast lookups to check for presence or absence of a specific edge, but it is slow to iterate over all edges.
- Adjacency lists use memory in proportion to the number edges, which might save a lot of memory if the adjacency matrix is sparse. It is fast to iterate over all edges, but finding the presence or absence specific edge is slightly slower than with the matrix.
Topological Sort
One of the most useful algorithms on graphs is topological sort, in which the nodes of an acyclic graph are placed in an order consistent with the edges of the graph. This is useful when you need to order a set of elements, for example, suppose you have a set of tasks to perform, but some tasks have to be done before other tasks can start. In what order should you perform the tasks? This problem can be solved by representing the tasks as nodes in a graph, where there is an edge from task 1 to task 2 if task 1 must be done before task 2. Then a topological sort of the graph will give an ordering in which task 1 precedes task 2. Obviously, to topologically sort a graph, it cannot have cycles.
A key observation in Topological Sorting is that a node finishes (is marked black) after all of its descendants have been marked black. Therefore, a node that is marked black later must come earlier when topologically sorted. For example, in the traversal example above, nodes are marked black in the order C, E, D, B, A. Reversing this, we get the ordering A, B, D, E, C. This is a topological sort of the graph. Interestingly enough, a postorder traversal generates nodes in the reverse of a topological sort.
Algorithm:
The algorithm for Topological sort is similar to DFS.
- We perform a depth-first search over the entire graph, starting anew with an unvisited node if previous starting nodes did not visit every node.
- As each node is finished (colored black), put it on the head of an initially empty list.
- This ensures that a node that is marked black later, appears at the head of the list.
- This clearly takes time linear in the size of the graph: O(|V| + |E|).
Detecting Cycle
We can use the idea of Topological sorting to detect a cycle in a graph. Since a node finishes after its descendants, a cycle involves a gray node pointing to one of its gray ancestors that hasn't finished yet. If one of a node's successors is gray, there must be a cycle.
To detect cycles in graphs, therefore, we choose an arbitrary white node and run DFS. If that completes and there are still white nodes left over, we choose another white node arbitrarily and repeat. Eventually all nodes are colored black. If at any time we follow an edge to a gray node, there is a cycle in the graph. Therefore, cycles can be detected in O(|V+E|) time.
Java Code:
In the example code below, the sample graph used is quite relatively dense and hence I use an adjacency matrix to represent the graph. To quickly look up a vertex, i enforce the following naming convention/lookup convention:
a b c d e f g h i j k
0 1 2 3 4 5 6 7 8 9 10
so the vertex 'a' is stored at index 0 in the array of vertices. An edge between vertex 'a' and 'b' would hence be an edge between 0 and 1.
A Vertex hence has a label/value and a state (initially white).
public int[][] matrix;
public Vertex[] vertices;
We store the list of vertices in an array and the graph is stored in an adjacency matrix.
You can find the full source code at:
https://github.com/sarveshsaran/ProgrammingSnippets/blob/master/GraphDFS.java
public int[][] matrix;
public Vertex[] vertices;
We store the list of vertices in an array and the graph is stored in an adjacency matrix.
You can find the full source code at:
https://github.com/sarveshsaran/ProgrammingSnippets/blob/master/GraphDFS.java



 RSS Feed
RSS Feed
